引   言 

齿轮是农业机械等机械上传动系统中的重要零件，其中弧齿锥齿轮因其大承载能力、平稳传动和高效率，被广泛用于两相交轴之间的动力传递，是实现高精度运动控制的关键部件。降低工作过程中齿轮接触应力以提升其可靠性是结构设计与开发中的关键。实践表明，仅仅提高制造和安装精度是不足以满足日益增长的对高性能齿轮的需求的，还会大大增加制造成本。合适的齿轮微观修形可有效提高其承载能力、延长使用寿命。因此，齿轮修形被广泛应用于提升齿轮传动的平稳性，是现代齿轮传动系统设计和制造的关键技术。

国内外许多研究人员针对齿轮修形优化进行了相关研究。WANGC等基于齿廓和齿向的综合修形，提出一种考虑减振降噪和齿面载荷均匀分布的斜齿轮多目标修形优化设计方法，优化后的齿根位置振动速度均方根值由1.2798×10^-4m/s降低至2.5875×10^-5m/s，齿面载荷差由15324N降低至47.956N。YANGJ等提出了一种修形人字齿轮传动激励的计算方法，通过齿廓修形和齿向修形会降低齿轮传动比和啮合刚度，螺旋角增大会减小啮合冲击力，随着修形量和修形长度的增加，啮合冲击减小。王承登等分析了齿轮修形对啮合冲击的影响，发现齿廓修形使啮合冲击位置发生变化，能有效减小冲击速度，随着修形量的增大，啮合冲击力减小。 MOHAMMEDO等提出一种结构化多目标优化方法，以五个方向上的修形量为设计变量，根据传动误差峰值和应力安全系数的权重得到了最终修形方案，有效减小了传动误差和应力水平。WEIX等提出一种用于稳健多目标优化准双曲面齿轮接触性能的方法，通过设计灵敏度分析验证了所提出方法的有效性，最终同时减小了传动误差峰值和齿面接触应力。莫帅等研究了不同齿廓修形量的齿轮传动系统动态特性变化，发现随着修形量的不断增加，齿轮的动态啮合力和动态传动误差等都呈现先降低后增大的现象，在修形量变化区间内确定了合理修形量并通过实验测试证明了合理修形后系统振动幅值降低。CHENP等通过预设齿面接触路径及传动误差等建立了二阶修形曲面，修形齿面的齿面接触应力、齿根弯曲应力及载荷分配等性能均满足设计要求。 聂少武等通过二阶多项式实现弧齿锥齿轮及准双曲面齿轮齿面拓扑修形，修形后齿面应力分布得到有效改善。NIES等用二阶曲面近似表示修形齿面与原始齿面之间的偏差，通过修改修形系数控制齿面形貌实现齿轮拓扑修形，修形后齿面接触应力、传动误差幅值均有降低，实验表明此修形方法可以实现驱动桥系统的减振降噪。在现有的研究中，通过修形方法降低直齿轮的接触应力、提升啮合平稳性的方法已经得到了广泛关注，但是由于弧齿锥齿轮齿面几何形状和啮合过程更为复杂，针对弧齿锥齿轮还需要进一步深入研究修形参数与齿轮啮合接触应力之间的关系，以进一步提高系统的可靠性。

本研究以某弧齿锥齿轮为研究对象，建立了齿轮啮合过程瞬态动力学模型，对齿轮啮合过程中的齿面接触应力进行了有限元计算，分析了修形参数对啮合应力的影响；建立了以齿轮接触应力为优化目标的齿轮修形参数优化模型，通过NSGA-II算法获得最优修形参数，有效降低了齿轮的接触应力。本研究对于提升弧齿锥齿轮可靠性具有较大的工程意义。

弧齿锥齿轮啮合瞬态动力学建模 

几何模型介绍： 

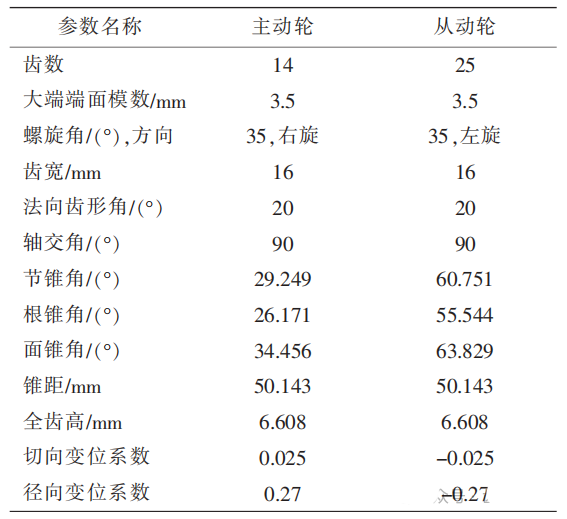
本文的研究对象为弧齿锥齿轮，该齿轮用于垂直轴系之间动力传递，其几何模型如图1，齿轮主动轮与从动轮的几何参数如表1所示。齿轮材料为20CrM_nTi，材料密度为7800kg/m³，弹性模量为207GPa，泊松比为0.25。

图 1 齿轮几何模型

表 1 齿轮几何参数

网格划分： 

对齿轮使用六面体网格单元进行划分。选择网格数量“齿廓70-齿向 50”的方案进行网格划分，划分结果如图2所示，最终网格数量为1308 220。

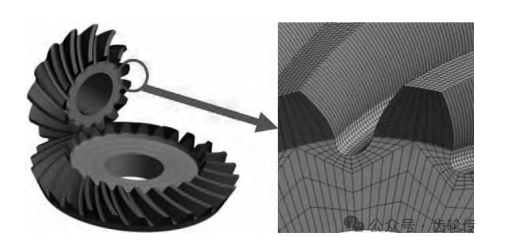
图 2 网格无关性验证及齿轮网格划分

有限元建模： 

使用LS-DYNA软件对齿轮啮合过程中的接触应力进行计算，将主从轮的齿面定义为接触对，主动轮齿面设置为接触面，从动轮齿面设置为目标面，根据ISO 10300—1:2023，在计算螺旋锥齿轮的载荷能力时不考虑摩擦，由此选择接触类型为“Frictionless”。在对齿轮传动接触的有限元分析中，通常采用主动轮施加转速、从动轮施加负载扭矩的方式来实现齿轮啮合传动接触，因此需要添加耦合齿轮内圈的对地转动副，并释放各自沿轴向旋转的自由度，以实现齿轮转速和负载扭矩的施加，转速和负载扭矩都采用斜坡加载在0.002s内完成，后续分析时长为齿轮转动一圈的时间即0.015s，计算总时间为0.017s。为保证齿轮接触分析收敛，将每个啮合位置的齿轮位置调整到刚好产生接触。

齿轮接触应力分析 

由于主动轮与从动轮应力分布规律相似，因此选取主动轮进行应力分布分析。啮合过程中齿轮接触应力分布如图3所示，图3中从左至右依次为啮入、啮合中期、啮出的齿面接触应力云图。由于齿轮发生了边缘接触，齿轮副接触应力始终处于较高水平，在啮出阶段，最大应力高达5595MPa，最大应力出现在齿顶位置。

图 3 主动轮接触应力

修形对齿轮接触应力的影响 

齿轮修形参数设计： 

由于弧齿锥齿轮副中小轮齿数少且加工时可调整参数多，针对小轮修形更容易提高修形效率，更容易达到理想的修形效果，因此本文针对主动小轮进行齿面拓扑修形。借助二阶曲面对齿面偏差拓扑的近似表达，将齿面拓扑分解为螺旋角修正、压力角修正、齿长曲率修正、齿廓曲率修正及齿面挠率修正等五个方向，通过改变五个方向的修形系数对齿面拓扑结构进行自由控制。因此本文的多目标优化设计变量为螺旋角修形量(a₁)、压力角修形量(a₂)、齿向鼓形修形量(a₃)、齿廓鼓形修形量(a₄)、齿面挠率扭曲修形量(a₅)，记为A={a₁，a₂，a₃，a₄，a₅}。设置螺旋角最大修形量为20μm，压力角最大修形量为55μm，齿向鼓形最大修形量为20μm，齿廓鼓形最大修形量为55μm，齿面挠率扭曲最大修形量为55μm。选择最小化接触应力(f₁)为目标函数，齿轮修形优化函数可写为：

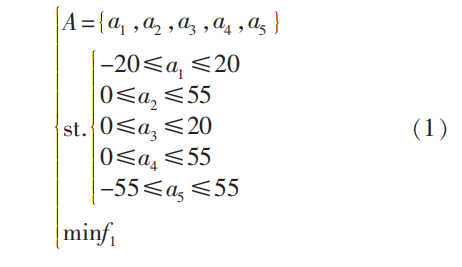
首先对弧齿锥齿轮修形方案进行试验设计(DOE)。使用最优拉丁超立方设计来计算试验设计空间的点，试验设计点的数量可根据输入设计变量的数量进行预估，其计算公式为：

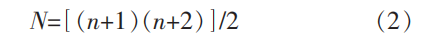
式中：N为最优拉丁超立方试验设计点数量，n为输入设计变量数。本文一共有5个设计变量，由式(2)计算可得设计点数量为21。为了更好地实现后续代理模型的构建及优化，本文选择30个试验设计点。 基于各设计变量的取值范围在ISIGHT软件的DOE模块中完成试验设计，基于各设计点的修形参数建立修形后的齿轮模型，进行齿轮啮合过程瞬态动力学计算。

修形参数对齿轮接触应力的影响: 

提取每种修形方案对应的最大接触应力，对计算结果进行灵敏度分析，获得修形参数对最大接触应力灵敏度的百分比(如图4所示)，图中数值为正表示正效应，数值为负表示负效应。五个方向上的修形参数均会对最大接触应力产生影响。影响齿面最大接触应力的设计变量依次为齿廓鼓形修形量(42.57%)、齿面挠率扭曲修形量(22.07%)、压力角修形量(15.29%)、螺旋角修形量(14.48%)、齿向鼓形修形量(5.59%)。齿廓鼓形对振动响应和最大接触应力都有较大的影响，可以初步判断通过齿廓鼓形修形可以更有效地改善应力及振动响应水平。由于应力对各因素的灵敏度均高于5%，因此各修形量对应力均有显著影响，关键在于最佳修形量的确定。

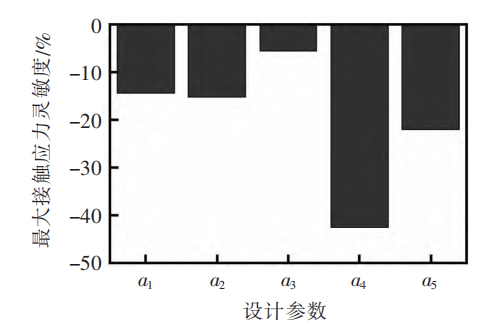
图 4 修形参数对目标函数的灵敏度

齿轮修形参数优化: 

基于所有修形方案的结果使用克里金模型构建代理模型，反映齿轮修形参数与最大接触应力的关系。本文代理模型在ISIGHT软件中选择克里金模型中的高斯函数构建。所构建的代理模型拟合R2值为0.933，平均相对误差为0.051，表明所构建的代理模型具有较好的拟合效果。基于上述的优化方案以及建立的代理模型，采用带有精英策略的非支配序列遗传算法(NSGA-II)实现弧齿锥齿轮修形参数优化。设置其种群规模为40，进化代数为400，交叉概率为0.9，交叉分布指数为10，变异分布指数为20。以最小化齿面最大接触应力为目标，对本文设置的优化目标进行迭代计算，最终获得弧齿锥齿轮修形参数。根据最优化修形参数，对齿轮啮合过程进行瞬态动力学分析，得到如图5所示的啮合过程中 齿面接触应力云图，从左至右依次为啮入、啮合中期、啮出的齿面接触应力云图，圆点所标处为最大接触应力点位置。

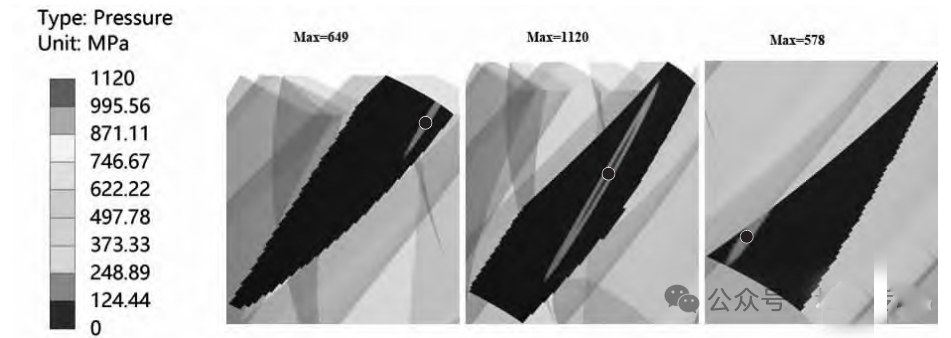
图 5 修形后主动轮接触应力

修形前后齿轮上最大接触应力在啮合过程中的变化曲线如图6所示，修形前后齿轮应力均呈现出周期性波动特征，波动周期与齿轮啮频一致。修形后齿面最大接触应力低于修形前齿面最大接触应力，尤其在啮合中后期更为明显，这是由于修形前齿面发生齿顶边缘接触，此处承载区域较小，齿面出现较高的应力。而采用优化的修形参数进行修形有效避免了边缘接触，从修形后接触应力云图可看出，齿面接触区域整体位于齿面中部呈现椭圆形，最大齿面接触应力位于接触椭圆区域中心，应力幅值为1120MPa。本文的修形方案有效优化了齿面接触区域分布与应力水平。

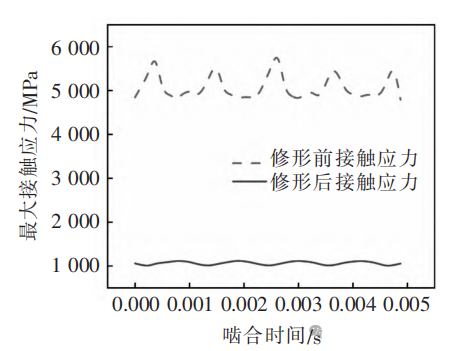
图 6 修形前后接触应力变化对比

  结   语 

针对某弧齿锥齿轮啮合过程中接触应力过大引起齿轮失效的问题，本文建立了弧齿锥齿轮啮合过程瞬态动力学有限元模型，分析了修形参数对齿面最大应力的影响，通过NSGA-II算法对齿轮修形参数进行优化，有效降低齿轮接触应力，获得如下主要结论。 

(1) 由于齿轮发生了边缘接触，齿轮副接触应力始终处于较高水平，在啮出阶段，最大应力高达5595MPa，最大应力出现在齿顶位置。 

(2) 影响齿面最大接触应力的修形参数依次为齿廓鼓形修形量、齿面挠率扭曲修形量、压力角修形量、螺旋角修形量、齿向鼓形修形量。 

(3) 采用优化的修形参数进行修形有效避免了边缘接触，齿面接触区域整体位于齿面中部呈现椭圆形，最大齿面接触应力位于接触椭圆区域中心，应力幅值为1120MPa，齿轮修形有效降低了齿轮接触应力。

参考文献：略。

作者简介：戴胡伟(1993—)，男，湖北咸宁人，工学博士，副研究员，主要研究方向为部件疲劳可靠性评估。