随着科技的快速发展，仿生机械研究已成为工程领域的重要方向。扑翼飞行器通过模仿鸟类和昆虫的飞行方式，具有更好的机动性、隐蔽性和能量效率。因此，仿生扑翼飞行器成为军事领域(军事侦察、巡逻、突袭、信号干扰等)和民用领域(环境监测、森林草原和农田上的火灾虫灾及空气污染等生态环境实时监测方面)研究的热点之一。扑翼飞行器的研究历史悠久，从早期的模型验证到如今的精准可控飞行，已取得了一系列的成果。Keennon等研制出具备彩色视频实时传输能力的仿蜂鸟扑翼飞行器。De等提出一种交叉X翼四翼面扑翼飞行器并研究其飞行控制。Folk⁃ertsma等利用3D打印技术制造出一款单段翼高速构型扑翼飞行器，并将其应用于机场驱鸟。Send等模仿鸟类的飞行特征研制出折叠翼扑翼飞行器SmartBird。德国 Festo公司模仿雨燕的翅膀特征研制出扑翼飞行器BionicSwift。Rose等研究六足爬行机器人和微小型扑翼飞行器二者的配合使用，实现扑翼飞行器的自主起飞。Chen等采用介电弹性体构造人工肌肉驱动微小型扑翼飞行器实现可控飞行。

在仿鸟类扑翼飞行器方面国内高校开展了大量研究并研制出一系列原型样机，包括西北工业大学的“信鸽”、南京航空航天大学的金鹰、哈尔滨工业大学的“凤凰”、北京航空航天大学的四翼面构型扑翼飞行器和双关节大鸟型扑翼飞行器、上海交通大学的基于电磁驱动和微机电系统的微小型扑翼飞行器，同时也在扑翼气动、驱动机构、飞行控制等多领域取得了一系列重大进展。X翼扑翼飞行器布局因其结构对称、受力均匀的特点成为扑翼微型飞行器设计中的重要方案之一。研究人员提出多种扑翼机构方案，包括曲柄滑块机构和空间连杆机构等。传统的连杆扑翼机构难以实现对扑翼运动的非对称调控，使得扑翼机器人在能量效率、负载能力及环境适应性等关键性能仍面临瓶颈。鉴于此，文中旨在设计一种仿鸟类扑翼运动特性的扑翼机构，利用非圆齿轮的传动特性来调控连杆机构的输出特性以实现X翼扑翼飞行器的非对称扑翼。

仿生扑翼机器人的设计与建模方法 

仿生扑翼机器人的整体结构:

图1所示为仿生扑翼机器人整体结构模型，主要由固定骨架、翅支驱动齿轮、非圆齿轮组等部件组成。固定骨架用来连接各传动部件，翅翼驱动齿轮、非圆齿轮组传递动力，固定骨架除用于支撑和连接外，可选择性安放驱动元件和传感器。在仿生扑翼机器人结构中，非圆齿轮副的主动轮1与从动轮11啮合传动，从动轮11与翅翼驱动齿轮2同轴，后驱动骨架6、前驱动骨架7组成X形结构，薄膜主骨架5、薄膜辅助骨架(90°)9、薄膜辅助骨架(45°)10共同组成薄膜4的支撑。仿生扑翼机器人飞行时，由非圆主动齿轮1提供动力，传递动力到非圆从动齿轮11，然后通过翅翼驱动齿轮带动后驱动骨架6和前驱动骨架7做往返运动，据此实现翅翼(即薄膜4)的张开及合拢运动，进而实现飞行。

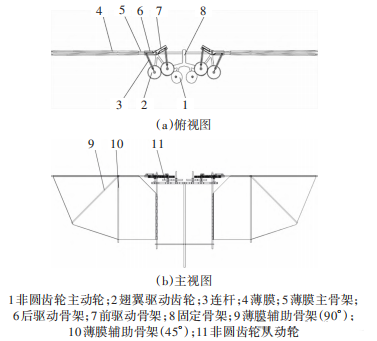
图1 仿生扑翼机器人整体结构

扑翼机构的数学模型: 

如图2和图3所示，翅翼驱动齿轮2、连杆3、前驱动骨架7及固定骨架8所组成的机构可简化成曲柄摇杆机构。

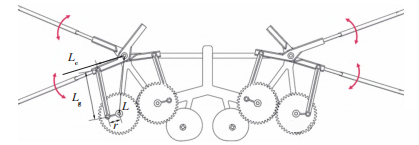
图2 曲柄摇杆运动分析图

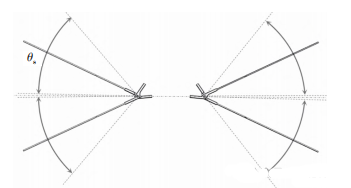
图3 翅翼运动边界图

根据四连杆机构的几何关系，可建立闭环方程以表示曲柄(翅翼驱动齿轮)转角θ_r与摇杆(前驱动骨架)转角θ_s的关系。假设固定骨架、曲柄、摇杆及连杆的长度分别为L，r，L_c和L_g，则连杆机构4个铰链的坐标分别为(0,0)，(L,0)，(rcos θ_r,rsin θ_r) 和(L+L_c cos θ_s,L_c sin θ_s)，故有：

约束方程为：

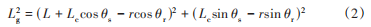
展开并简化方程：

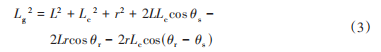
进一步整理为Freudenstein方程形式：

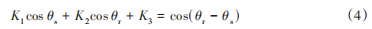
其中，常数由杆长确定：

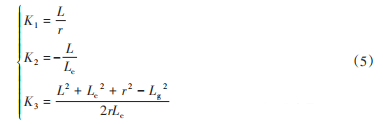
非圆齿轮副的设计: 

在仿生扑翼机器人的结构中，非圆齿轮副在实现非对称扑翼过程中尤为重要。图4为其节曲线啮合示意图，当主动轮匀速旋转一周时，从动轮也会相应旋转一周，且做一次增速和一次减速运动。O₁和O₂为回转中心，θ₁和θ₂分别为主动轮和从动轮的回转角度，r₁(θ₁)和r₂(θ₂)分别为主动轮和从动轮节曲线，E为中心距。文中将非圆齿轮副的传动比周期θ_T分为两个传动区间，区间A上的传动用于实现非对称扑翼运动特性，区间B上的传动则用于确保运动周期的连续性。假设非圆齿轮传动比函数为：

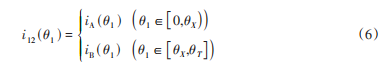
式中：i_A(θ₁)——非圆齿轮副在区间A上的传动比函数；

i_B(θ₁)——非圆齿轮副在区间B上的传动比函数； 

θ_X——两个传动区间的分界点； 

θ_T——传动比函数的周期。

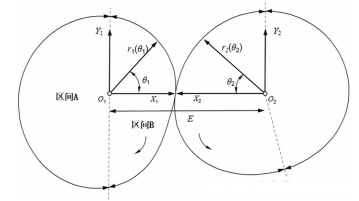
图4 非圆齿轮的啮合坐标系

非圆齿轮节曲线封闭条件为：

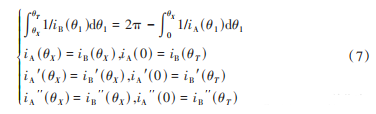
式中：θ_T=2_π；

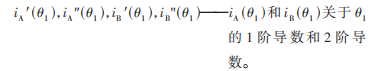
虽然有较多的研究表明非对称的扑翼方式能够提高扑翼机器人的升力，然而何种具体的扑翼规律具有最佳的气动性能还未有定论，鉴于分段多项式函数具有较好的灵活性，文中选择该类函数构造非圆齿轮副的传动比。i_A(θ₁)的选取根据非对称扑翼运动特性设定，文中假设i_A(θ₁)为反比例函数，即：

式中：a，b——给定的系数。此外，假设i_B(θ₁)可表示为：

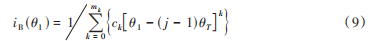
式中：m_k——多项式的次数；

c_k——多项式的系数。

根据式(6)~式(9)，若m_k给定，则可求解出c_k，从而求得传动比函数i₁₂(θ₁)。非圆齿轮节曲线以极坐标形式表示为：

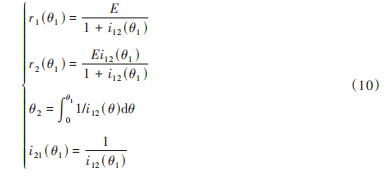
设计算例 

仿生扑翼机器人运动算例分析中，假设翅翼为刚性结构，且齿轮结构传动不存在延迟，完全同步。参考现有的X翼型扑翼机器人，设置初始参数如表1所示。

表1 初始参数 mm 

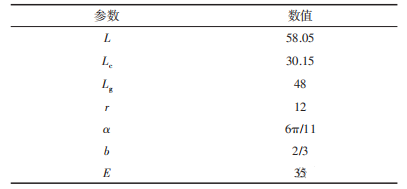
其中，L，L_c，L_g，r为改进前的初始参数；a，b，E为改进后加入的非圆齿轮参数。将数据代入式(6)~式(10)中解出非圆齿轮节曲线和非圆齿轮传动比函数，如图5所示，中心距E为35mm，求解得到的非圆齿轮主动轮节曲线与从动轮节曲线相啮合。如图6所示为求解得到的非圆齿轮传动比与主动轮转角的关系。将数据代入式(1)解出曲柄摇杆机构的关系后，结合计算所得的非圆齿轮传动比，获得扑翼机器人翅翼改进前后的角速度关系。如图7所示，其中，角速度取正值，添加非圆齿轮改进后在翅翼张开时(齿轮转角0°~150°，300°~360°)，角速度峰值下降约18.2%；而在翅翼合拢时(齿轮转角 150°~300°)，角速度峰值提高约21.5%，进而实现鸟类扑翼时“快扑慢回”运动模仿。

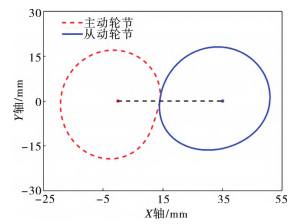
图5 非圆齿轮节曲线啮合图

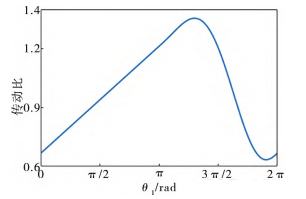
图6 非圆齿轮副传动比与θ1关系图

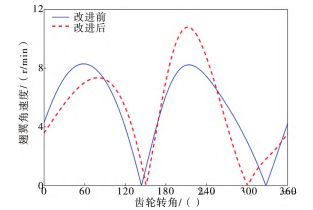
图7 翅翼角速度对比图

运动仿真分析 

采用SolidWorks软件仿真模拟仿生扑翼机器人在无外界干扰条件下的扑翼姿态，以验证上文非圆齿轮对翅翼飞行姿态调控的可行性。在SolidWorks的Motion插件中建立仿生扑翼机器人模型，如图8所示。仿真过程中重点关注非圆齿轮的变传动比对曲柄摇杆机构的摇杆输出角度的影响，因此，在仿真过程中，将驱动源设置为非圆齿轮机构的从动轮，并且去除了无关 的部件以减少计算量。

图8 仿生扑翼机器人模型

为对比仿生扑翼机器人加入非圆齿轮机构前后的姿态，直观表现非圆齿轮对扑翼机器人的影响，设置X翼初始夹角为60°，设计生成两个Motion算例，分别将驱动源设置为恒定的转速3.33r/min及变化的转速3.33i₂₁r/min。在这两个motion算例中仿真后，得到机器人在不同转角下的身体姿态。如图9和图10分别为电机转动角度到325°时改进前后的姿态，当电机转到325°时，改进前的机器人到极限位置，而改进后的机器人已经越过极限位置增大一定角度。

图9 电机转角325°改进前机器人扑翼姿态

图10 电机转角325°改进后机器人扑翼姿态

机器人改进前后的角位移曲线如图11所示。对翅翼合拢时(150°~300°)和翅翼张开时(0°~150°，300°~360°)的角度变化，翅翼角位移最大值处，改进后较改进前滞后约5°；最小值处改进后较改进前提前约25°。改进后合拢区间缩短到约 150°，张开区间扩大到约210°，由于主动轮为恒速，可知齿轮角位移与时间呈线性关系，从而可知X翼每一次合拢及张开运动，合拢所需时间缩短约17%，张开所需时间增加约17%。仿真结果表明，改进后的翅翼变化姿态验证了非圆齿轮可以调控仿生扑翼机器人扑翼的运动规律。本研究中改变的运动规律为：X翼以较高角速度合拢，以较低的角速度张开。

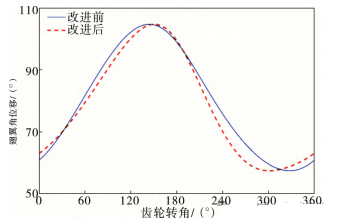
图11 翅翼角位移对比图

  结   论 

文中提出了一种实现仿生扑翼运动的非对称扑翼机构，该机构由非圆齿轮组与曲柄摇杆机构组合设计。非圆齿轮的变传动比特性能够对曲柄摇杆机构的输出特性进行调控，从而实现鸟类扑翼时“快扑慢回”非对称运动的模仿。主要结论如下： 

1）基于SolidWorks的运动仿真结果表明，改进后的扑翼机构在翅翼合拢时角速度峰值显著提升，在翅翼张开时角速度峰值降低，验证了非圆齿轮对扑翼时序的非对称调控能力。 

2）提出的非圆齿轮传动为仿生扑翼机器人的机构设计提供了一种非对称的扑翼方案，可通过调整齿轮节曲线参数适配不同翼展与扑动频率需求，具有一定的工程应用潜力。 

3）由于所提出的机构主要聚焦于非对称扑翼的运动学调控，因此在分析中假设所有构件为刚性的，未考虑柔性翼面的气动弹性效应、真实飞行环境中的流场干扰及构件的强度设计等。在后续工作中将结合流固耦合仿真与实物样机试验，进一步探究动态升力、运动稳定性、负载等关键性能。

参考文献：略。

作者简介：肖小平(1995—)，男，副教授，博士，研究方向：机器人、机械设计及理论。