引   言 

随着工业机器人、新能源车等产业的迅速发展，对高性能齿轮传动系统提出了更高的要求。面对设备的传动精度、准确性、效率和使用寿命等问题，人们迫切需要一种高效精密的齿轮制造方法。如今，高精齿轮的加工已经由单一的剃齿、磨齿、珩齿变成了现在剃齿和珩齿或者珩齿和磨齿协同加工的复杂工艺。但是齿面精加工前的热处理，会出现齿轮变形问题，导致后续精加工困难。为了降低其加工难度，提高加工精度、效率和使用寿命等，需要研究滚齿修形技术，实现滚齿对加工余量的控制。因此，建立滚齿加工余量控制模型，对齿轮精加工前预修形具有重要意义。

滚齿工艺是基于展成法的圆柱齿轮高效切削加工工艺，主要用于齿轮半精加工。为了获得滚齿加工齿轮齿面，学者们进行了很多研究。Dimitriou等开发了一个软件程序，用于齿轮的滚齿加工过程仿真，并得到了切屑和剩余工作齿轮的连续实体几何。Simon建立了斜齿轮滚齿过程的数学模型，以此确定齿面的微观形貌，并讨论了轴向进给、最大螺纹数等加工参数对最大齿面偏差的影响。Nico等通过几何穿透计算模拟滚切过程，确定了未切削的切屑几何形状，并与有限元模拟相结合，确定了切削力和切削温度的分布。Yang等开发了高速干式滚刀数字化可视化的数学模型，建立了精确的三维切屑几何形状。Chen等编写了滚刀加工的生成齿面的几何形貌预测的程序，用以对高速干式滚齿的齿面形貌进行数值模拟，并分析了加工参数对齿面形貌的影响。Han等提出了一种基于多轴联动控制的齿面拓扑修形方法，该方法通过建立轴的运动多项式函数，通过各轴之间的联动达到齿轮修形的效果。Tran等将机床轴的运动以多项式形式表示，建立了机床轴设置对齿轮法向偏差的灵敏度矩阵，并结合LM算法获得所需多项式系数，提出了一种数值方法的闭环拓扑修形方法。韩江等基于复合修形叠加曲线，提出了一种齿轮拓扑修形方法，以传动误差峰峰值最小化为目标，通过遗传算法优化修形参数。

综上所述，国内外专家对齿轮修形工艺进行了卓有成效的研究，为滚齿预修形提供了 一定的借鉴，但主要集中在齿面修形对齿轮啮合状态和齿面扭曲现象的改善。本文旨在改善精加工前余量不均的现象，基于滚齿工艺运动学原理推导了滚齿成形齿面方程，建立滚齿预修形数学模型；将Y、B轴的运动表示为含有(ζ，φ_h)的二阶多项式来实现齿面的修形；通过微调修形参数求解敏感度矩阵，使用动态规划算法优化修形参数，实现了精加工前齿面任意加工余量的控制，通过实例仿真验证了该方法的有效性，为滚齿预修形提供了理论依据。

滚齿成形齿面数学建模 

在滚齿加工过程中，滚刀和工件齿轮相当于一对空间交错轴齿轮相互啮合，利用它们之间的强制啮合进行滚切，同时滚刀沿轴向进给形成全齿宽。根据滚齿加工工艺原理，建立了滚齿成型齿面数学模型，如图1所示。

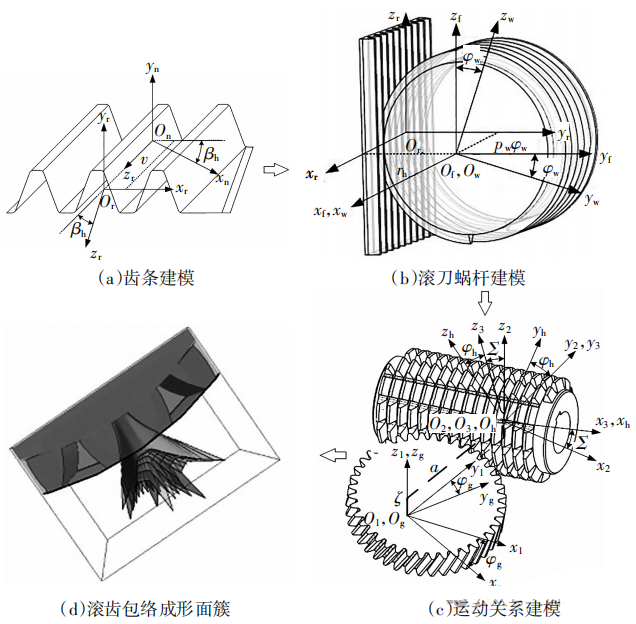
图1 滚齿成形数学模型

图1为滚齿成形齿面建模过程，首先由齿条共轭啮合得到基本蜗杆，然后通过对其开槽形成滚刀前角和退屑槽，最后由滚刀齿面包络形成工件齿面曲面簇，由此得到成形齿面方程rg。图1(c)中包含了5个坐标系，分别为滚刀和工件的固定坐标系S(O_2x2y2z2)、S(O_1x1y1z1)和滚刀辅助坐标系S(O_3x3y3z3)以及运动坐标系S(O_hxhyhzh)、S(O_gxgygzg)；滚刀和工件固定坐标系原点沿y轴方向的距离为中心距a，沿z轴方向的距离为轴向进给量ζ，滚刀绕y₂轴旋转的角度为轴交角∑；滚刀和工件分别绕x₃与z₁做同步回转运动的转角分别为φ_h、φ_g。

根据滚刀和工件啮合运动关系，通过坐标变换得到工件的齿面方程：

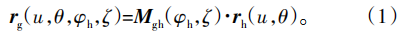
式中：r_h为滚刀齿面方程，M_gh为变换矩阵。

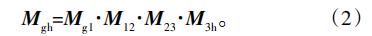
基于齿轮啮合原理，可知工件成形齿面是滚刀曲面簇的包络，由于存在两个独立运动参数φ_h和ζ，滚刀和工件的啮合方程满足：

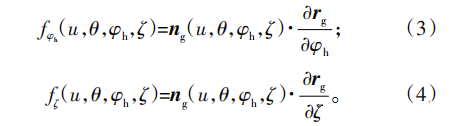
式中，n_g为齿面法向量。

滚齿预修形方法 

滚齿机床运动学模型: 

滚齿机床主要包括6个运动轴，即滚刀回转轴A、切向运动轴X、沿工件轴向进给轴Z、径向进给轴Y、刀架回转台轴交角调整轴B、工件齿轮的回转轴C，滚齿机床结构如图2所示。为了实现齿面修形，需要滚齿机多轴联动控制。工件齿轮回转轴C(φ_g)和滚刀回转轴A(φ_h)固定传动比运动，滚刀径向进给运动轴Y(a₁)和刀架回转台轴交角调整轴B(∑₁)分别与滚刀轴向进给轴Z(ζ)和滚刀回转轴A进行联动运动，其运动关系如下。

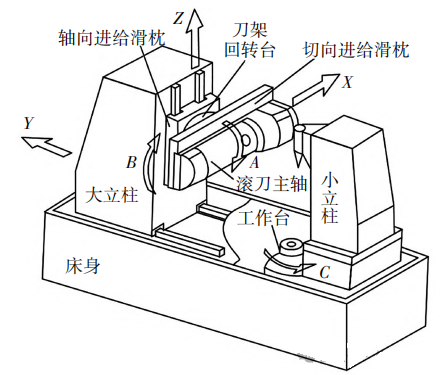
图2 机床结构简图

C轴和A轴的运动关系为

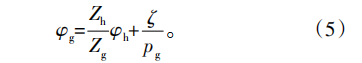
式中：Z_g、Z_h分别为工件和滚刀的齿数，p_g为齿轮螺旋参数。

Y轴和A、Z轴的运动关系为

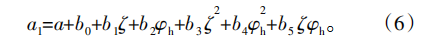
B轴和A、Z轴的运动关系为

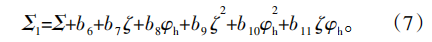
式中，多项式系数b₀~b₁₁为修形参数。

齿面修形法向加工余量及敏感度矩阵:

为了获得齿面修形的数值数据，在齿面测量区域定义了35个网格点，其中5个点从齿顶到齿根依次分布在齿廓上，7个点依次沿齿向方向分布在齿宽上，如图3所示。 

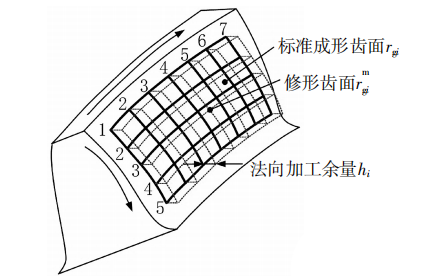
图3 齿轮齿面网格

齿面网格点的法向加工余量通过以下等式确定：

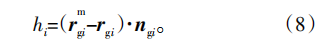
式中：r_gi和r^m_gi分别为滚齿标准成形齿面和滚齿修形齿面，可联立式(1)、式(3)、式(4)求解得到；n_gi为网格点处的滚齿加工标准成形齿面的法向矢量，h_i为网格点i处的法向加工余量。通过微调修形参数可以得到其对齿面各网格点处余量的影响程度，这里以敏感度矩阵U表示。

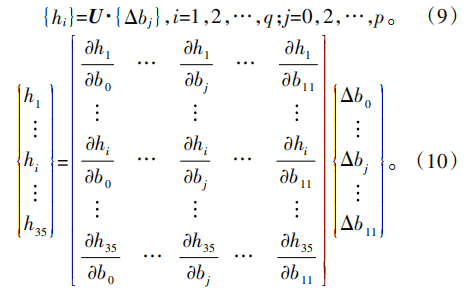
式中：q=35为选取的35个网格点；p=11为式(6)、式(7)中的12个修形参数；Δb_j表示第j个参数的变化值；矩阵U中的∂h_i/∂b_j为敏感系数，表示该参数变化对该点的法向加工余量的影响程度。

 实例仿真计算及优化 

使用上述滚齿预修形方法对实例进行数值仿真计算，以探究多项式系数对齿面修形的影响分析并验证所提方法的可行性。滚刀和工件齿轮的基本参数如表1所示。 

表1 滚刀和工件齿轮基本参数

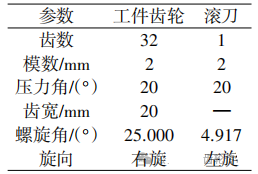
通过逐个微调多项式系数b₀~b₁₁，设置其最小变化单位量为0.001，联立式(10)即可求解敏感度矩阵U部分如式(11)所示。

分析式(11)可知，齿面修形B轴的影响程度要显著高于Y轴。各多项式系数相对应网格点处的法向加工余量如图4所示。其中∑δ表示齿面35个网格点的法向加工余量之和。由图4(a)、图4(c)、图4(e)、图4(g)～图4(i)可知，改变运动参数φ_h的系数，齿形方向的法向余量发生改变；而改变运动参数ζ时，齿形方向法向余量和齿向方向法向余量均发生改变。并且2阶的影响程度都要显著高于0阶和1阶的影响程度。

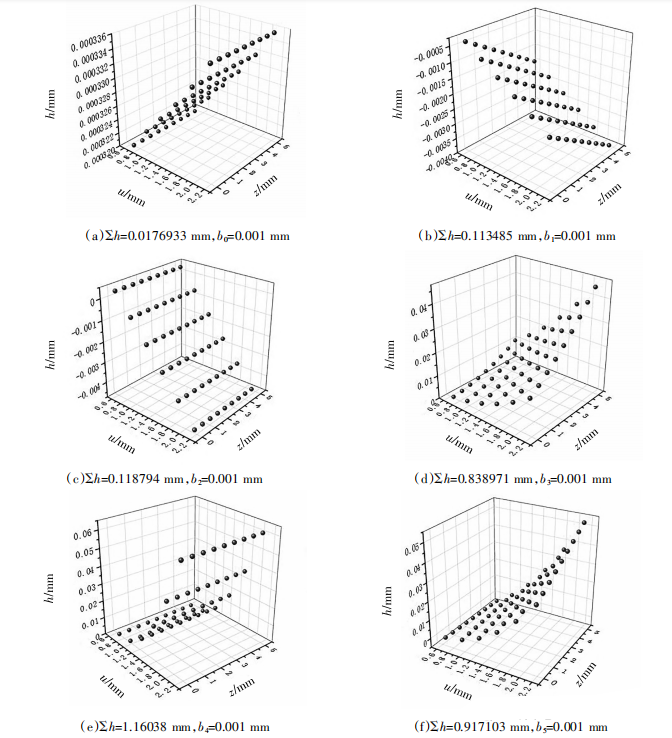
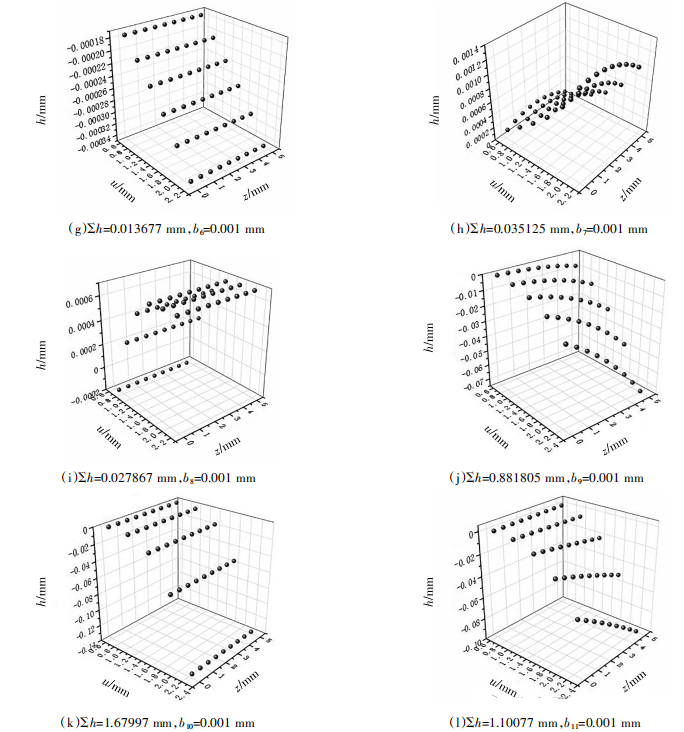
图4 各多项式系数相对应修形齿面的法向加工余量

给定目标修形齿面的修形量如表2所示，通过式(10)、式(11)求得的敏感度矩阵即可反求出修形参数。式(10)中的修形参数个数远小于网格点的个数，属于超定方程组，求解的精度过低。动态规划是一种进行顺序优化的通用技术，通过多阶段求解决策过程最优化过程，可降低其复杂性，提高计算效率，因此采用动态规划算法对其进行优化计算，建立了齿面预修形模型。

表2 给定齿面各点修形量 mm

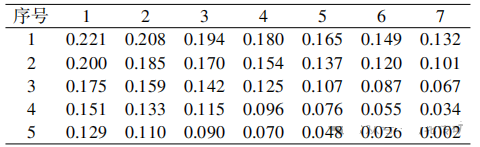
1）将优化修形参数的过程分为多个阶段的优化问题。 

2）各阶段的修形参数作为优化变量l_n，将式(10)计算所得各参数作为初始值，优化变量l_n的取值范围为：

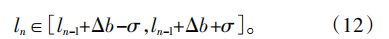
式中：l_n为第n个阶段的各修形参数，σ为l_n的变化范围。

3）对于n过程，将当前实际齿面作为状态变量r_n，状态转移方程为

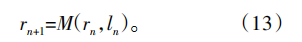
式中：M为修形过程，修形后的齿面r_n+1由修形前齿面r_n和修形参数l_n决定。 

4）以当前修形齿面和目标修形齿面各网格点处法向偏差总和为阶段评价指标c_i(r_i，l_i)：

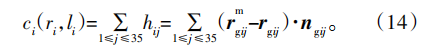
式中：r^m_gij和r_gij分别为实际修形齿面和目标修形齿面网格点的位置矢量，n_gij为目标修形齿面的法向矢量。

5）指标函数C_n衡量优化过程的好坏，即修形齿面和目标修形齿面法向偏差总和最小。

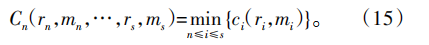
修形参数优化过程如图5所示。 

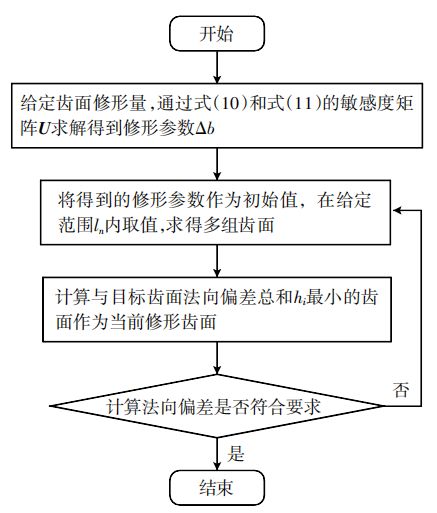
图5 修形参数优化流程图

目标修形齿面如图6(a)所示；初始修形齿面如图6(b)所示；经过动态规划算法优化的修形齿面如图6(c)所示，其法向加工余量如表3所示；优化前后修 形误差对比结果如图6(d)所示，敏感度矩阵求解修 形参数的修形误差最大为0.4023mm，平均修形误差为0.0291mm，各点修形误差方差为0.00099；动态规划算法最大修形误差不超过0.0087mm，平均修形误差为0.0022mm，各点修形误差方差为0.00001。最 终优化修形参数所对应的修形齿面修形量如表3所示。

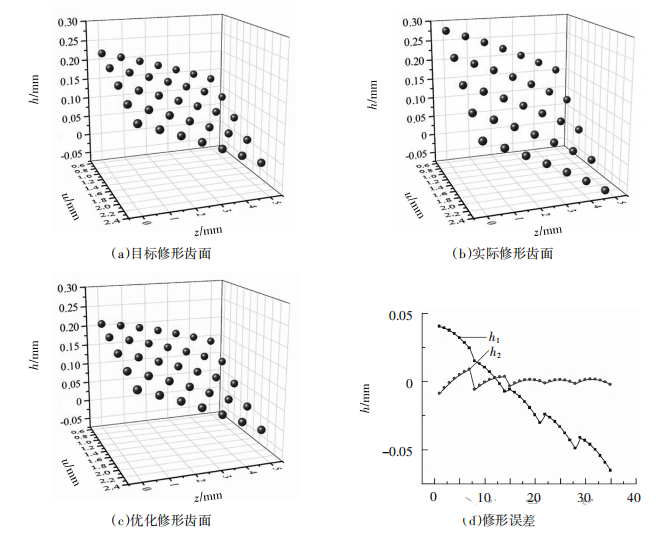
图6 优化修形结果

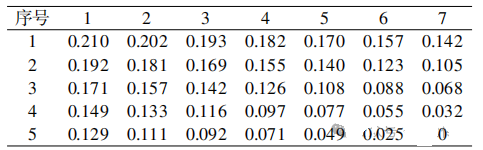
表3 优化修形齿面各点修形量 mm

  结   语 

本文根据滚齿加工原理，提出了一种多轴联动的滚齿预修形方法，通过数值计算得到了修形参数对法向加工余量的影响规律，并能任意修形齿面，为齿轮精加工前的预修形提供了理论依据。主要内容如下。 

1）基于滚齿工艺的运动学原理和齿轮啮合原理建立了滚齿成形齿面数学模型。

2)建立了滚齿机床运动学模型,将机床、B轴的运动表示为含有(ζ，φ_h)的二阶多项式函数,建立了滚齿预修形齿面的数学模型。

3）微调Y、B轴各修形参数 ，分析了各参数对齿面法向加工余量的影响,得到了敏感度矩阵U。

4)根据给定的目标修形齿面,利用动态规划算法对修形参数进行优化计算,数值仿真结果表明,本文提出的修形方法适用于滚齿预修形，修形误差较小且余量分布均匀。

参考文献：略。

作者简介：阳国万(1998—)，男，硕士研究生，研究方向为齿轮先进制造工艺与装备；